几千字的流水账真的会有人从头看到尾吗(?
不按作业的要求顺序来了,有意思的放最前,重要的放其次,其余的往后排。
我们真的需要一台电梯么?
首先,回顾一下作业要求:我们要模拟六台电梯的运行、调度,和其开关门、移动、对乘客的接、送行为,其中大部分行为需要等待一定的现实时间。而评测要求我们在每一状态转移完成时输出一条信息,以供测评评测机中模拟的电梯状态机是否在符合正确性规范的前提下完成功能,并评测性能。
为什么是状态机
Everything is a state machine.
经常上OS的同学都知道,状态机是一种表示可数个(我想表达的意思是,可以依据规律枚举、列举出,即使有无限种)状态以及在这些状态之间的转移和动作等行为的数学模型。
我们看该单元的电梯系统的架构设计:绝大部分同学(不如说难道还有用其他架构的吗)采取的是这样一种“三段式架构”:
$$输入线程 \rightarrow 请求队列 \rightarrow 分配器线程 \rightarrow 等待队列 \rightarrow 电梯线程$$当然,根据大家设计的不同,可能还有其他的共享对象或者其他的箭头关系(主要取决于应对电梯踢人OUT-F和接受临时调度、Update等奇葩请求的设计)。
而电梯是如何决策其状态转移的呢?电梯有如下状态等:当前楼层,是否开门,等待(下称pending)队列,电梯内乘客队列(下称current)。在第一次作业我们就实现了这样一个状态机:采用ALS, LOOK, 或者其他的什么算法。我采用的是出于优先级考虑的,在高覆盖率的同时降低加权平均等待时间的改进的LOOK算法。
executions的引入
那么,这一状态机的输入是什么?
回顾我们的架构设计,理所当然的,我们会说:输入当然是分配器分配给该电梯的等待队列,吗?
事实上,其决策并不依赖输入,换言之,并不是只有有新的请求时电梯才会动的。即使没有请求,电梯也会把自己唤醒,逐步更新自己的状态,直到回归pending和current都变为空的状态。
也就是说,在任一时刻,若假定该状态机不再会有新的输入(不再分配新的请求),那我们就能推演出该状态机的后续所有行为。 所以,在后文中,我们暂且规定,称“状态机”为这种没有输入的,自动决策状态转移的状态机。 有没有很像上学期计组做的那个CPU,把机器码记录在文件中加载出来,就能自动执行状态转移?如果把CPU和记录机器码的存储设备框在一起,而不认为机器码是一种输入。把机器码比作pending和current中的数据,和这一单元的电梯是不是很像?
那我们还该如何定义“分配新请求”这种行为呢?很简单,每次分配了新请求,或者告诉电梯要进行SCHE或UPDATE时,我们可以重新计算一遍该电梯从当前状态作所有决策,直到回归空闲状态这一区间中,所有的状态转移,并将其更新给电梯线程,电梯线程依次执行即可。
这里,我们引入一个队列 LinkedList<Executeable> executions。用以存储当前电梯所有的状态转移行为,依次执行完就可以抵达名为空闲的终点。
Interface Executeable,要求实现方法execute(Elevator elevator); 执行时实现状态转移,更新电梯的当前状态
解构一台电梯
我们实现了对电梯这一对象的逐步解构:现在你还可以坚持称电梯线程在模拟一台电梯,实际上它在做的事情只有:计算executions,execute执行,或者当时间条件不满足时await()。
下述是对该电梯完全解构的最后一步:把计算executions的工作交给分配器
为什么要这么做?这么做有什么好处?我们考虑分配器的如下分配策略:
- 分配器现在需要分配某乘客请求给六台电梯中的任一台,如果可以的话,它希望知道分配给具体哪一台电梯能获得最优性能。(当然,不可以的话,随机挑一台塞进去也不是不能跑)
- 既然对分配器想要分配的这一时刻来说,每一台电梯的接下来的所有行为都是已知的,那么每一台电梯接下来的行为可以用以计算其成本。
- 那么,分配器想知道分配给哪一台电梯能让总成本最低,就会依次尝试把乘客请求分配给其中某一台电梯的情况,并希望知道其总成本:这样,选出总成本最低的一种情况,不就是局部的、已知的最优策略了么。相当于在若干条时间线,选了最完美的一条。
- 但是,怎么知道每一台电梯接下来的行为,甚至是,每一台电梯在接受了当前乘客请求的这一IF线下,接下来的行为呢?我们刚才已经讨论过了,既然是状态机,那么必然是可以计算的。
- 把电梯线程叫醒帮自己计算看上去不太现实(事实上也不太现实),那就自己计算吧,把六个状态机的状态拷贝一份,再创造六个接受了当前乘客分配的IF线状态机,选出最好的一条IF线,并拿这个IF线状态机替换掉真正的状态机,狸猫换太子,就实现了最优分配策略。
- 那,算都算完了,电梯线程偷个懒不算了,拿着分配器算好的executions,到时间就执行并且输出就好了。
影子电梯:但是只有影子电梯
至此,这一臃肿的、模拟真实电梯运行的线程的工作,只剩下:维护一个状态已知、接下来所有状态转移已知的状态机,到了时间就给状态机执行一步状态转移并输出,没到时间就回去等着。
那么,电梯还存在吗?或许游离于分配器的心中,或许藏匿于状态机的状态里,又或许闪烁在评测机的眼中,反正不可能说它存在于电梯线程的模拟中了,这么说电梯线程也不能答应的,它只是拿着一串executions,到时间就输出出来而已,连execute都是封装好的。所以我称这样的“电梯线程”为
Class Printer extends Thread,它就是一台到时间就自动打印的打印机而已。
按道理来说,贴代码是没人有心思看的,自己的代码自己迭代时都懒得读,但是这是这个线程所剩下的全部内容了,还是读一下吧? 为可读性优化和简化了部分,所以算伪代码。
public void run() {
long lastTime = System.currentTimeMillis();
lock.lock();
// 为方便读,这里省掉了await的try-catch包装块。
while (true) {
ExecuteAble execution = null;
// 瞬间的行为,循环依次完成。
while (!executions.isEmpty()) {
execution = executions.getFirst();
if (needTimeToExecute(execution)) {
break;
}
lastTime = executeAndUpdate(execution, lastTime);
}
// 空闲状态,尝试结束或等待新任务的分配。
if (executions.isEmpty()) {
if (end) { break; }
MainProcess.signalDispatcher();
printable.await();
continue;
}
// 非瞬间行为,判断是否满足执行条件,失败则等待。
long timeToWait = lastTime
+ needTimeMap.get(execution)
- System.currentTimeMillis();
if (timeToWait <= 0) {
lastTime = executeAndUpdate(execution, lastTime);
} else {
printable.await(timeToWait, TimeUnit.MILLISECONDS);
}
}
lock.unlock();
}
于是,我们实现了所谓影子电梯,证明了影子电梯的可行性,但是全部都是影子电梯。与其说分配器是通过影子电梯计算出分配给具体哪一台真正的电梯,不如说分配器是拿一台更新后的影子电梯换掉了原来的影子电梯。
既然影子电梯可行,如何适应性能指标?
现在谈谈该调度策略是如何权衡总时间、加权平均时间和电量的:
- 首先,我们要尽量降低总时间$T_{run}$:这一性能指标显然比另外两个重要的多,如果为追求低功耗而$T_{run}$过大,我们甚至会被判断为效率太低而超时,而平均分配、随机分配等方法,也都是在放弃对于加权平均时间和功耗的考量下,追求$T_{run}$的解法。
但是,$T_{run}$有两个特性:
- 一是对于所有电梯来说,只有最大的$T_{run}$是有意义的,当其中一台电梯的总时间很长,而给其他某台电梯分配了请求后总时间依然不比最长的总时间长,那么$T_{run}$是没有变化的,此时追求降低$T_{run}$是一种没太大意义的行为。
- 二是对于当前$T_{run}$最大的电梯来说,捎带请求是一种以牺牲少量$T_{run}$换取极大加权平均时间和功耗上收益的决策。代价是你需要花额外0.4s的$T_{run}$在这一层停下并开关门,性能上却相当划算。
因此,在六台电梯分别接受分配请求的时间线中,我选出所有接受分配请求后,$\Delta T_{run} \leq 1s$的时间线并纳入考虑,如果没有符合条件的,则选出$T_{run}$增加值最小的一种情况直接作为分配结果。
接下来我们就可以不考虑$T_{run}$对性能的影响了,即使还有影响,也不到1s,可以大致忽略。我们要考虑,经过筛选后的若干种情况里,加权平均时间$wT$和功耗$W$综合最优的一种情况。但由于性能分是与同学们排名后计算的,我并不知道怎样取得综合最优,理论上我们需要满足:
$$\begin{align*} \Delta \text{cost} &= a \Delta wT + b \Delta W, \quad a + b = 1 \\ \begin{pmatrix} a & b \end{pmatrix} &= \arg\min \Delta \text{cost} \end{align*}$$我取$\begin{pmatrix} a & b \end{pmatrix} = \begin{pmatrix} \frac{10}{10+1} & \frac{1}{10+1} \end{pmatrix}$,最后效果尚可。
双轿厢:线程协作是否应该影响对象行为?
我们已经论述过了,时间是线程(具体来讲,是Printer这一打印机线程)要考虑的,线程是动态的、连续的,共享对象只有状态,是静态的、瞬间的。
所以双轿厢电梯的行为,是共享对象所考虑的,同步开始改造和避免相撞却是线程所需保证的。
具体来讲,我们采取的策略是到达临界楼层后,通过锁等方式让协作线程若有需求先等待自己完成任务,自己完成后尽快退出临界楼层(当然该行为也是共享对象所存储的,而非线程唤起的),放还锁让协作线程继续动态行为。
而在同步改造方面:
- 当两电梯的下一execution均为
UPDATE-BEGIN时,由分配器输出UPDATE-BEGIN并唤醒两打印机线程进入计时。两线程共享一把锁。 - 其中一台电梯
UPDATE-BEGIN时锁上共享锁,UPDATE-END时先输出UPDATE-END,然后放还共享锁。 - 另一台电梯不输出,
UPDATE-BEGIN时无行为,但UPDATE-END时先尝试拿到共享锁,拿到后立即放还,然后才执行自己的后续操作。 - 这样,我们就实现了两协作线程的同步。
在这一过程中,线程间的交互不对对象状态产生影响,只对状态转移的时间,即线程行为有所限制。故而,线程协作不影响对象行为。
接下来补充比较重要的内容。
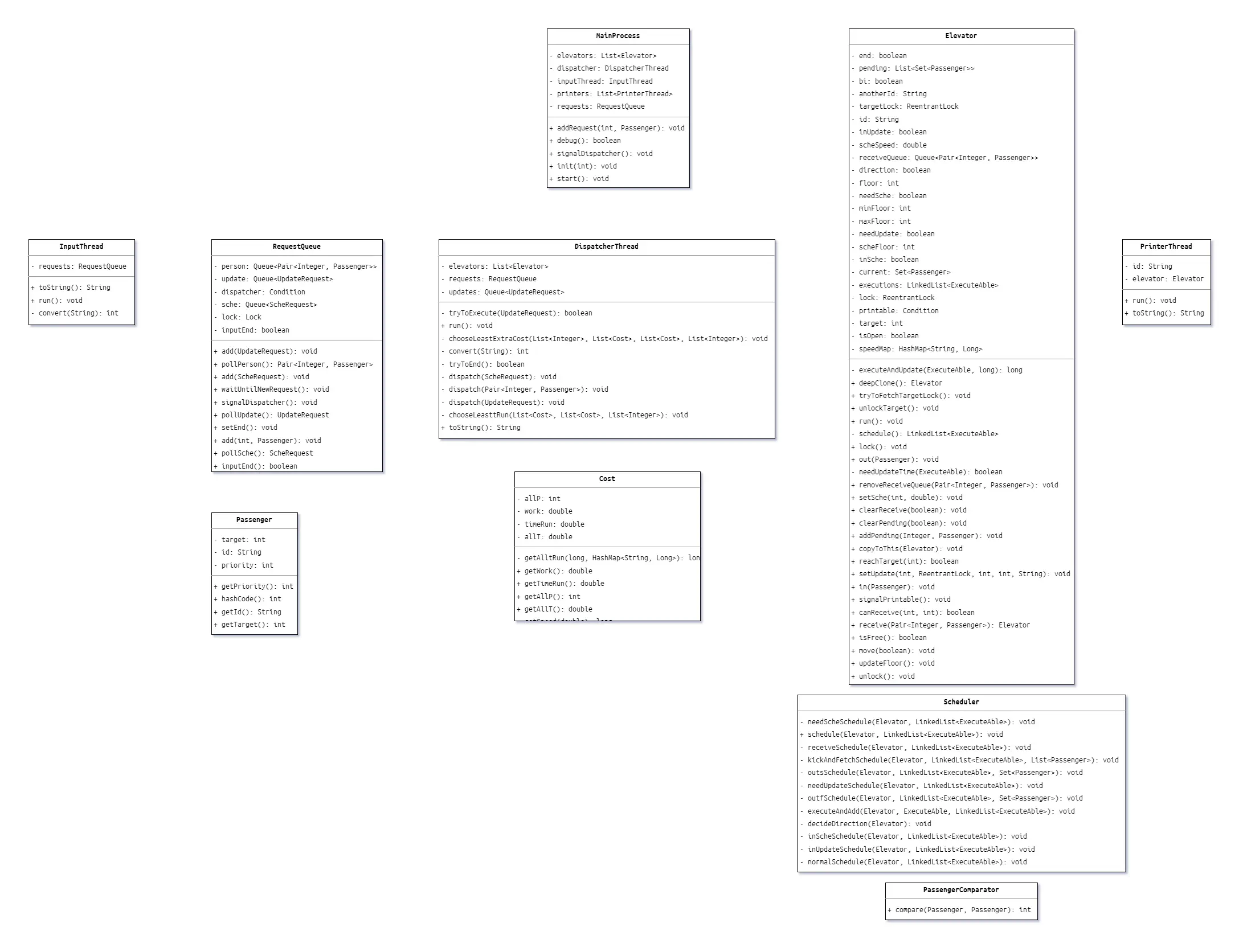
架构设计
很明显能看出三段的设计:$线程-共享对象-线程-共享对象-线程$。
前文已介绍过该架构的工作流程,在第一次作业中,我采用与大家相同的架构,而在第二次作业的重构中,我将电梯线程的功能解构提取,变成了如上的只保留简单功能的PrinterThread。第三次作业中,无新增类。
值得介绍的是Scheduler类,其包装了该状态机的决策行为,也即其所有的状态转移计算过程。通过封装Scheduler,我们实现了电梯决策器的可拓展性:当我们需要更换、优化电梯算法,只需要换一个Scheduler或者继承原Scheduler即可。
这里给出一种性能优化思路,配备多种Scheduler,考虑每种电梯装载不同Scheduler,采取不同算法的时间线,并综合总的性能考量,返回给各状态机最优的executions。但该方法的计算量预估提升了一个数量级,为避免CTLE,应谨慎考虑。
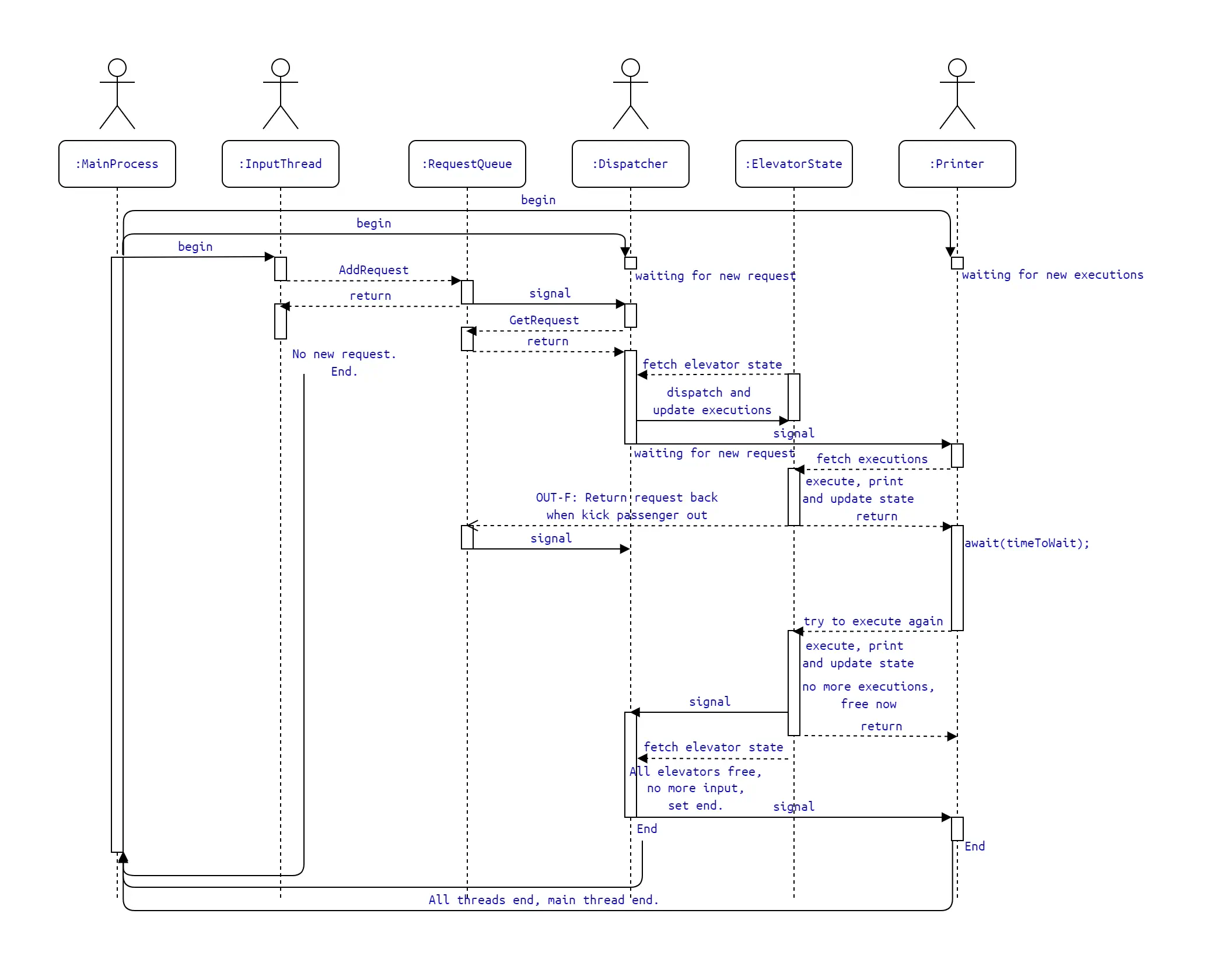
线程协作
上图已明了介绍线程中的协作关系,此处详细解释最后的线程结束的判定:- 首先,输入线程的结束条件很清晰:读取到值为
null的请求时。 - 但对于Request Queue来说,输入线程与六个电梯线程同时作为生产者,分配器作为消费者;同时,对于每个电梯状态机,分配器是生产者,电梯线程是消费者。
- 这就形成了一个圈:分配器与电梯互为消费者和生产者,而生产者没有结束时,消费者自然不可以结束。
- 因此,我们重新定义电梯线程作为生产者的结束:当其executions为空,即空闲状态下,它自然不可能再放归新的请求,我们可以认为其处于临时的结束状态。
- 而对于此时的调度器,倘若没有需要分配的请求,其会尝试结束:
- 输入线程已结束
- 各电梯线程处于空闲状态
- 也即对于RequestQueue,不会有新的生产,也因此没有消费行为和消费行为导致的新的生产。
- 此时调度器可以认为达到结束条件,结束自身线程并对后续所有线程设置结束。
有趣的和重要的均已结束,现在补充作业要求的其他内容。
易变的内容
稳定的内容已于上文完成分析,而易变的内容,我们需着眼分析两个“例外”:SCHE和UPDATE。
- 对于
SCHE,我选择将ScheBegin和ScheEnd纳入Executeable范畴,将其视为状态机的正常状态转移行为,从而使其回归稳定的内容的体系; - 对于
UPDATE大体相同,但UPDATE-BEGIN实在太特殊,为了两电梯之间的同步,我将其设置为电梯的一种新的状态并因此补充了大量特判,这也是引发我bug的直接原因:补丁没打全。
Bug分析与Debug方法
第一二次作业无bug,对第三次作业的UPDATE-BEGIN处理引发了第三次作业的bug,并直接导致了强测爆炸:
对于UPDATE-ACCEPT前分配给电梯的请求,经过改造后并不一定能接受,因为其所在楼层不一定属于自己所能移动的范围内。而为了避免UPDATE和SCHE之间无法RECEIVE请求导致分配器轮询,我为每个电梯配置RECEIVE请求缓存区,囤积在END后再输出,因此错过了UPDATE-BEGIN时清空当前已RECEIVE请求的机会,从而可能RECEIVE改造后无法处理的请求。
改正方法为:UPDATE开始时清除RECEIVE缓存区中自己改造后无法处理的请求。
Debug方法为输出。当debug模式启用时,输出各关键行为前后的线程状态、状态机状态。
// MainProcess.java
public static boolean debug() { return false; }
虽然本次作业没有要求课程建议,但是实在很想建议:
能不能给一个
TimableOutput.debug(String string)然后输出内容不计入评测,只供debug时便于人类查看,间接解决掉评测出的bug在本地无法复现的问题?这样只要写好关键步骤的日志,就能快速定位到bug,即使本地无法复现也可以正常修复?
线程安全与层次化设计
- 锁的合理使用
- 在本次作业中,线程安全是至关重要的。尤其是在处理多线程的电梯调度和状态更新时,锁的使用非常关键。例如,在电梯线程和分配器线程之间共享的状态机状态(如电梯的当前楼层、电梯内乘客队列等)必须通过锁来保证线程安全。
- 我们使用了
ReentrantLock来确保在更新状态时不会出现竞态条件。例如,在电梯线程执行状态转移时,需要对executions队列进行操作,此时必须加锁,防止分配器线程同时修改该队列。同时,锁的使用也需要谨慎,避免死锁的发生。在电梯线程和分配器线程之间,我们通过合理的锁顺序和锁的释放时机来避免死锁。 - 使用
ReentrantLock有什么好处?条件管理更灵活,而且锁可以脱离对象或代码块而存在,请看使用了ReentrantLock的影子电梯的名场面六把锁:
elevators.forEach(Elevator::lock);
// 计算与分配
elevators.forEach(Elevator::unlock);
- 线程间通信的同步机制
- 线程间通信的安全性也是线程安全的重要方面。在本次作业中,电梯线程和分配器线程之间通过
executions队列进行通信,而这个队列的更新和读取必须是线程安全的。 - 我们使用了
Condition来实现线程间的同步。例如,当电梯线程处于空闲状态时,它会调用await()等待分配器线程的信号。分配器线程在计算出新的executions后,会调用signal()唤醒电梯线程。这种同步机制确保了线程间通信的正确性和及时性。 - 同时,在处理双轿厢电梯的同步(改造期间)与互斥(临界楼层)时,我们通过共享一把
ReentrantLock来实现两台电梯线程之间的同步。这种同步机制不仅保证了线程安全,还避免了电梯之间的冲突。
- 线程间通信的安全性也是线程安全的重要方面。在本次作业中,电梯线程和分配器线程之间通过
- 架构设计的层次化
- 层次化设计使得代码更加清晰和易于维护。在本次作业中,我们将整个电梯系统划分为多个功能模块,每个模块负责特定的功能。
- 例如,输入线程负责读取请求并将其放入请求队列;分配器线程负责从请求队列中取出请求并分配给电梯;电梯线程负责执行电梯的状态转移。这种模块划分使得每个线程的功能单一,便于理解和维护。
- 同时,我们还引入了
Scheduler类来封装电梯的状态转移计算逻辑。这样,当需要更换或优化电梯算法时,只需要修改Scheduler类,而不需要修改电梯线程的代码。这种层次化设计提高了代码的可扩展性和可维护性。